Generally, as a programmer you don't need to concern yourself about operationsat the bit level. You're free to think in bytes, or ints and doubles, or evenhigher level data types composed of a combination of these. But there aretimes when you'd like to be able to go to the level of an individual bit.Exclusive-or encryption is one example when you need bitwise operations.

• Drivers Bitwise Practice
• Drivers Bitwise Operators
• Drivers Bitwise Jobs
• Drivers Bitesquad.com
• Drivers Bitwise App

The following operators perform bitwise or shift operations with operands of the integral numeric types or the char type: Unary (bitwise complement) operator Binary (right shift) shift operators Binary & (logical AND)(logical OR), and ^ (logical exclusive OR) operators.

Another example comes up when dealing with data compression: what if youwanted to compress a file? In principle, this means taking one representationand turning it into a representation that takes less space. One way of doingthis is to use an encoding that takes less than 8 bits to store a byte. (Forinstance, if you knew that you would only be using the 26 letters of the Romanalphabet and didn't care about capitalization, you'd only need 5 bits to doit.) In order to encode and decode files compressed in this manner, you needto actually extract data at the bit level.

Jan 21, 2020 Here are the 5 Business Drivers for your Data Warehouse Migration to Cloud. Managing and Deriving Value from Big Data. Cloud providers offer plenty of tools for extracting structured, semi-structured and unstructured datasets, loading those datasets into cloud repositories, and making the data available for transformations (the extract-load-transform ELT paradigm). Driver crashes into Bitwise 41 building in downtown Fresno Fresno police are searching for a driver who crashed into the Bitwise 41 building downtown Fresno on Monday morning. Hit-and-run driver.

Finally, you can use bit operations to speed up your program or perform neattricks. (This isn't always the best thing to do.)

Thinking about Bits

The byte is the lowest level at which we can access data; there's no 'bit' type, and wecan't ask for an individual bit. In fact, we can't even perform operations ona single bit -- every bitwise operator will be applied to, at a minimum,an entire byte at a time. This means we'll be considering the wholerepresentation of a number whenever we talk about applying a bitwise operator.(Note that this doesn't mean we can't ever change only one bit at a time; itjust means we have to be smart about how we do it.) Understanding what itmeans to apply a bitwise operator to an entire string of bits is probablyeasiest to see with the shifting operators. By convention, in C and C++ youcan think about binary numbers as starting with the most significant bit tothe left (i.e., 10000000 is 128, and 00000001 is 1). Regardless of underlyingrepresentation, you may treat this as true. As a consequence, the results ofthe left and right shift operators are not implementation dependent forunsigned numbers (for signed numbers, the right shift operator isimplementation defined).
The leftshift operator is the equivalent of moving all the bits of a number aspecified number of places to the left:For instance, consider the number 8 written in binary 00001000. If we wantedto shift it to the left 2 places, we'd end up with 00100000; everything ismoved to the left two places, and zeros are added as padding. This is thenumber 32 -- in fact, left shifting is the equivalent of multiplying by apower of two.Note that in this example, we're using integers, which are either 2 or 4bytes, and that the operation gets applied to the entire sequence of 16 or 32bits.
But what happens if we shift a number like 128 and we're only storing it in asingle byte: 10000000? Well, 128 * 2 = 256, and we can't even store a numberthat big in a byte, so it shouldn't be surprising that the result is 00000000.
It shouldn't surprise you that there's a corresponding right-shift operator:>> (especially considering that I mentioned it earlier). Note that abitwise right-shift will be the equivalent of integer division by 2.
Why is it integer division? Consider the number 5, in binary, 00000101. 5/2is 2.5, but if you are performing integer division, 5/2 is 2. When youperform a right shift by one: (unsigned int)5>>1, you end up with 00000010, as therightmost 1 gets shifted off the end; this is the representation of the number2. Note that this only holds true for unsigned integers; otherwise, we arenot guaranteed that the padding bits will be all 0s.
Generally, using the left and right shift operators will result insignificantly faster code than calculating and then multiplying by a power oftwo. The shift operators will also be useful later when we look at how tomanipulating individual bits.
For now, let's look at some of the other binary operators to see what they cando for us.

Bitwise AND

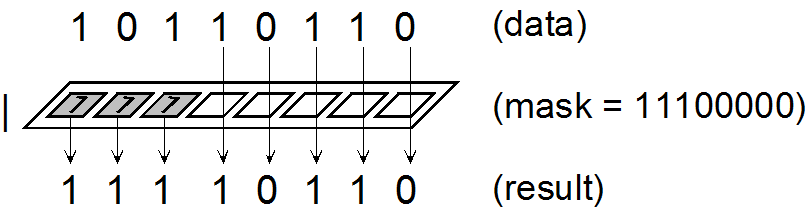
The bitwise AND operator is a single ampersand: &. A handy mnemonic isthat the small version of the boolean AND, &&, works on smaller pieces(bits instead of bytes, chars, integers, etc). In essence, a binary ANDsimply takes the logical AND of the bits in each position of a number inbinary form.
For instance, working with a byte (the char type):The most significant bit of the first number is 0, so we know the mostsignificant bit of the result must be 0; in the second most significant bit,the bit of second number is zero, so we have the same result. The only timewhere both bits are 1, which is the only time the result will be 1, is thefifth bit from the left. Consequently,

Bitwise OR

Bitwise OR works almost exactly the same way as bitwise AND. The onlydifference is that only one of the two bits needs to be a 1 for thatposition's bit in the result to be 1. (If both bits are a 1, the result willalso have a 1 in that position.) The symbol is a pipe: |. Again, this issimilar to boolean logical operator, which is ||.and consequentlyLet's take a look at an example of when you could use just these fouroperators to do something potentially useful. Let's say that you wanted tokeep track of certain boolean attributes about something -- for instance, youmight have eight cars (!) and want to keep track of which are in use. Let'sassign each of the cars a number from 0 to 7.
Since we have eight items, all we really need is a single byte, and we'll useeach of its eight bits to indicate whether or not a car is in use. To dothis, we'll declare a char called in_use, and set it to zero. (We'll assumethat none of the cars are initially 'in use'.)Now, how can we check to make sure that a particular car is free before we tryto use it? Well, we need to isolate the one bit that corresponds to that car.The strategy is simple: use bitwise operators to ensure every bit of theresult is zero except, possibly, for the bit we want to extract.
Consider trying to extract the fifth bit from the right of a number: XX?XXXXXWe want to know what the question mark is, and we aren't concerned about theXs. We'd like to be sure that the X bits don't interfere with our result, sowe probably need to use a bitwise AND of some kind to make sure they are allzeros. What about the question mark? If it's a 1, and we take the bitwiseAND of XX?XXXXX and 00100000, then the result will be 00100000:Whereas, if it's a zero, then the result will be 00000000:So we get a non-zero number if, and only if, the bit we're interested in is a1.
This procedure works for finding the bit in the nth position. The only thingleft to do is to create a number with only the one bit in the correct positionturned on. These are just powers of two, so one approach might be to dosomething like:While this function works, it can be confusing. It obscures the fact thatwhat we want to do is shift a bit over a certain number of places, so that wehave a number like 00100000 -- a couple of zeros, a one, and some more zeros.(The one could also be first or last -- 10000000 or 00000001.)
We can use a bitwise leftshift to accomplish this, and it'll be much faster toboot. If we start with the number 1, we are guaranteed to have only a singlebit, and we know it's to the far-right. We'll keep in mind that car 0 willhave its data stored in the rightmost bit, and car 7 will be the leftmost.Note that shifting by zero places is a legal operation -- we'll just get backthe same number we started with.
All we can do right now is check whether a car is in use; we can'tactually set the in-use bit for it. There are two cases to consider:indicating a car is in use, and removing a car from use. In one case, we needto turn a bit on, and in the other, turn a bit off.
Let's tackle the problem of turning the bit on. What does this suggest weshould do? If we have a bit set to zero, the only way we know right now toset it to 1 is to do a bitwise OR. Conveniently, if we perform a bitwise ORwith only a single bit set to 1 (the rest are 0), then we won't affect therest of the number because anything ORed with zero remains the same (1 OR 0 is1, and 0 OR 0 is 0).
Again we need to move a single bit into the correct position:What does this do? Take the case of setting the rightmost bit to 1: we havesome number 0XXXXXXX | 10000000; the result, 1XXXXXXX. The shift is the sameas before; the only difference is the operator and that we store the result.
Setting a car to be no longer in use is a bit more complicated. For that,we'll need another operator.

The Bitwise Complement

The bitwise complement operator, the tilde, ~, flips every bit. A useful wayto remember this is that the tilde is sometimes called a twiddle, and thebitwise complement twiddles every bit: if you have a 1, it's a 0, and if youhave a 0, it's a 1.
This turns out to be a great way of finding the largest possible value for anunsigned number:0, of course, is all 0s: 00000000 00000000. Once we twiddle 0, we get all 1s:11111111 11111111. Since max is an unsigned int, we don't have to worry aboutsign bits or twos complement. We know that all 1s is the largest possiblenumber.
Note that ~ and ! cannot be used interchangeably. When you take the logicalNOT of a non-zero number, you get 0 (FALSE). However, when you twiddle anon-zero number, the only time you'll get 0 is when every bit is turned on.(This non-equivalence principle holds true for bitwise AND too, unless youknow that you are using strictly the numbers 1 and 0. For bitwise OR, to becertain that it would be equivalent, you'd need to make sure that theunderlying representation of 0 is all zeros to use it interchangeably. Butdon't do that! It'll make your code harder to understand.)
Now that we have a way of flipping bits, we can start thinking about how toturn off a single bit. We know that we want to leave other bits unaffected,but that if we have a 1 in the given position, we want it to be a 0. Take some time to think about how to do this before reading further.
We need to come up with a sequence of operations that leaves 1s and 0s in thenon-target position unaffected; before, we used a bitwise OR, but we can alsouse a bitwise AND. 1 AND 1 is 1, and 0 AND 1 is 0. Now, to turn off a bit,we just need to AND it with 0: 1 AND 0 is 0. So if we want to indicate that car 2 is no longer in use, we want to take the bitwise AND of XXXXX1XX with 11111011.
How can we get that number? This is where the ability to take the complementof a number comes in handy: we already know how to turn a single bit on. Ifwe turn one bit on and take the complement of the number, we get every bit onexcept that bit:Now that we have this, we can just take the bitwise AND of this with thecurrent field of cars, and the only bit we'll change is the one of the car_numwe're interested in.You might be thinking to yourself, but this is kind of clunky. We actuallyneed to know whether a car is in use or not (if the bit is on or off) before we canknow which function to call. While this isn't necessarily a bad thing, itmeans that we do need to know a little bit about what's going on. There is aneasier way, but first we need the last bitwise operator: exclusive-or.

Bitwise Exclusive-Or (XOR)

There is no boolean operator counterpart to bitwise exclusive-or, but there isa simple explanation. The exclusive-or operation takes two inputs andreturns a 1 if either one or the other of the inputs is a 1, but not if bothare. That is, if both inputs are 1 or both inputs are 0, it returns 0.Bitwise exclusive-or, with the operator of a caret, ^, performs theexclusive-or operation on each pair of bits. Exclusive-or is commonlyabbreviated XOR.
For instance, if you have two numbers represented in binary as 10101010 and01110010 then taking the bitwise XOR results in 11011000. It's easier to seethis if the bits are lined up correctly:You can think of XOR in the following way: you have some bit, either 1 or 0,that we'll call A. When you take A XOR 0, then you always get A back: if A is1, you get 1, and if A is 0, you get 0. On the other hand, when you take AXOR 1, you flip A. If A is 0, you get 1; if A is 1, you get 0.
So you can think of the XOR operation as a sort of selective twiddle: if youapply XOR to two numbers, one of which is all 1s, you get the equivalent of atwiddle.
Additionally, if you apply the XOR operation twice -- say you have a bit, A,and another bit B, and you set C equal to A XOR B, and then take C XOR B: youget A XOR B XOR B, which essentially either flips every bit of A twice, ornever flips the bit, so you just get back A. (You can also think of B XOR Bas cancelling out.) As an exercise, can you think of a way to use this toexchange two integer variables without a temporary variable? (Once you'vefigured it out, check the solution.)
How does that help us? Well, remember the first principle: XORing a bit with0 results in the same bit. So what we'd really like to be able to do is justcall one function that flips the bit of the car we're interested in -- itdoesn't matter if it's being turned on or turned off -- and leaves the rest ofthe bits unchanged.
This sounds an awful lot like the what we've done in the past; in fact, weonly need to make one change to our function to turn a bit on. Instead ofusing a bitwise OR, we use a bitwise XOR. This leaves everything unchanged,but flips the bit instead of always turning it on:

When should you use bitwise operators?

Bitwise operators are good for saving space -- but many times, space is hardlyan issue. And one problem with working at the level of the individual bits isthat if you decide you need more space or want to save some time -- forinstance, if we needed to store information about 9 cars instead of 8 -- thenyou might have to redesign large portions of your program. On the other hand,sometimes you can use bitwise operators to cleverly remove dependencies, suchas by using ~0 to find the largest possible integer. And bit shifting tomultiply by two is a fairly common operation, so it doesn't affect readabilityin the way that advanced use of bit manipulation can in some cases (forinstance, using XOR to switch the values stored in two variables).
There are also times when you need to use bitwise operators: if you're workingwith compression or some forms of encryption, or if you're working on a systemthat expects bit fields to be used to store boolean attributes.

Summary

Drivers Bitwise Practice

You should now be familiar with six bitwise operators:
Works on bits for left argument, takes an integer as a second argument

Drivers Bitwise Operators

Shifts bits to of bit_arg shift_arg places to the left -- equivalent tomultiplication by 2^shift_argShifts bits to of bit_arg shift_arg places to the right -- equivalent tointeger division by 2^shift_arg
Works on the bits of both arguments

Drivers Bitwise Jobs

Takes the bitwise AND of left_arg and right_argTakes the bitwise XOR of left_arg and right_argWorks on the bits of only argumentReverses the bits of arg
Skills and knowledgeYou also know a couple of neat tricks that you can use when performance iscritical, or space is slow, or you just need to isolate and manipulateindividual bits of a number.
And you now should have a better sense of what goes on at the lowest levelsof your computer.

A Parting Puzzle

One final neat trick of bitwise operators is that you can use them, inconjunction with a bit of math, to find out whether an integer is a power of two.Take some time to think about it, then check out the solution. Related articles

Drivers Bitesquad.com

A bit of background in bits and a few other tricks

Drivers Bitwise App